Hey Reader !!! In this post we will understand about the sorting methods of Data-Structure in Java

Contents include

What is sorting algorithm?
Why sorting algorithm?
Types of sorting algorithm?
Description of each type of sorting algorithms

What is Sorting Algorithm ?

Sorting is the process of arranging elements of an array according to the comparison operator [ less than || greater than || equal to ] of an element, so that elements can be placed either in ascending order or descending order.

The comparison operator is used to decide the new order of element in the respective Data-Structure.

Why sorting algorithm?

Sorting as important in programming as how we do in our everyday life. It is easier and faster to locate the items if it is in sorted order.
In algorithms the sorting can be mainly used for searching or adding data in sorted format to a file or a report and many more.

Types of Sorting algorithm :

Bubble sort
Selection sort
Insertion sort
Cycle sort
Merge sort
Quick sort
Heap sort

Bubble sort :

Bubble sort is known as the simplest sorting algorithm.
In bubble sort — array is traversed from first element to the last element.
Bubble sort compares the current element with the next element.
If the current element is greater than the next element, then swap the element.
In bubble sort, as the size of the array/input increases the number of comparison will also increase.
Bubble sort algorithm is slow in performance — reason is as the excessive comparison and swapping, since it compares each element of array to another and swaps.
Bubble sort is best suited for small or less number of elements or data

How Bubble sort works:

Consider an unsorted input array — array[] input = {5, 3, 8, 4, 6}
Bubble sort starts with very first two elements, comparing which one is greater.
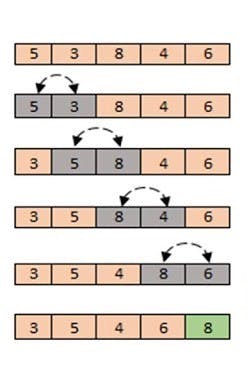
If the second element is greater than the first element then, swap the element.
Complexity and Performance of Bubble sort algorithm
Bubble sort Best case comparison — O(n) where the given array is sorted array- ex : { 1, 2, 3, 4, 5}
Bubble sort Worst case comparison — O(n²) where the given array is not sorted array- ex : {5, 4, 3, 2, 1}

Example Code:

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

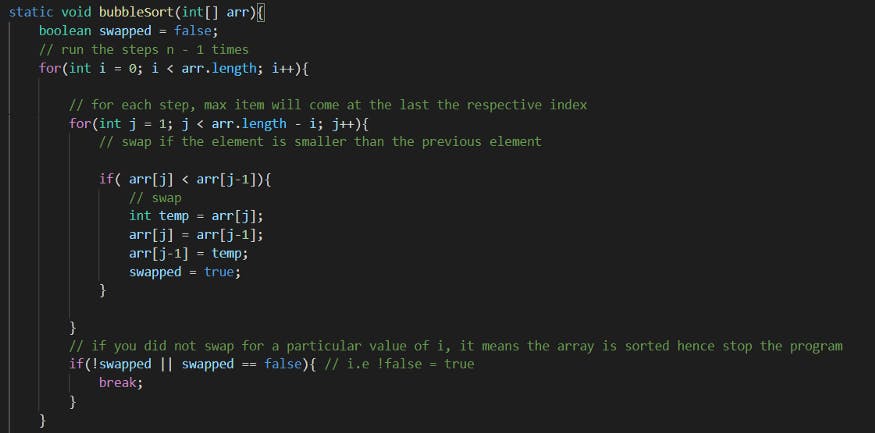
2. Selection Sort

Selection sort is one of the simple sorting algorithm where we are going to select an element and place it the right index / position.
The selection sort algorithm sorts the array by finding the minimum element from an unsorted array and putting it at the beginning [ in case of ascending ]
The selection sort maintains two subarrays
The sorted array - the beginning
The unsorted array - the end values
In every iteration of selection sort, the minimum element is picked and moved to the beginning of the array.

How Selection Sort works :

Consider an unsorted input array - array[] input = {4, 5, 1, 2, 3}

Selection sort, starts with finding the largest element in the array = 5
Swap with the right index
max value = 5

swap with correct index = 3

                   4, 5, 1, 2, 3
                   4, 3, 1, 2, 5                       n -1

max value = 4

swap with correct index = 2

                   4, 3, 1, 2, 5
                   2, 3, 1, 4, 5                         n - 2

max value = 3

swap with correct index = 1

                    2, 3, 1, 4, 5
                    2, 1, 3, 4, 5                          n -3

max value = 2

swap with correct index = 1

                    2, 1, 3, 4, 5
                    1, 2, 3, 4, 5                           n - 4

Time and space complexity of Selection sort:

Best time complexity = O(n²) Worst time complexity = O(n²)

In Code explanation

Find the max value :

private static int getMaxIndex(int[] arr, int start, int end) {
        int max = start;
        for (int i = start; i <= end; i++) {
            if (arr[max] < arr[i]) {
                max = i;
            }
        }
        return max;
    }

Sort the given array

static void selectionSortAlgorithm(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            /* find the max item in the remaining array and 
swap with correct index */

            int lastElement = arr.length - i - 1;
            int maxIndex = getMaxIndex(arr, 0, lastElement);

            // we got the maxIndex, now swap the element
            int temp = arr[maxIndex];
            arr[maxIndex] = arr[lastElement];
            arr[lastElement] = temp;
        }
    }

Insertion Sort

Insertion sort is one of the simple sorting algorithm.
Insertion sort works similar to the sorting of playing cards
Example : Consider you have a set of cards, in that the first card is already sorted [a smaller number], then we select an unsorted card, if the selected unsorted card is greater than the first card, it will be placed at the right side otherwise it will be placed at the left side.
Similarly all unsorted cards are taken and put in their exact place to make the sorted array.
In insertion sort, all the sorted elements are placed at the left hand side and unsorted elements will be at the right hand side.
Each element from the right hand side is compared with the element of the left hand side.

How Insertion sort works

Consider an unsorted array - arr[] input = {5, 3, 4, 1, 2}
At all the time j > 0 and i must be ≤ n - 2
Sort the array till the ith value

Step 1 :  for i = 0 , j = 1
                              5, 3, 4, 1, 2

Step 2 : for i = 1, j = 2
                                       5, 3, 4, 1, 2
                              j = 1       
                                       3, 5, 4, 1, 2

When element j is not smaller than the element j - 1, break the loop

Step 3 : for i = 2, j = 3
                                       3, 4, 5, 1, 2
                            j = 2
                                       3, 1, 4, 5, 2
                           j = 1
                                       1, 3, 4, 5, 2

Now, for i = 2 till index 3 it is sorted

Step 4 : for i = 3, j = 4
                                       1, 3, 4, 5, 2
                             j = 3        
                                       1, 3, 4, 2, 5
                             j =2  
                                       1, 3, 2, 4, 5
                             j = 1
                                       1, 2, 3, 4, 5

the value of i will always be array.length - 2, because j value will be equal to i +1;
if i length is not equal to array.length - 2, the jth value will be given as ArrayIndexOutOfBoundException

Why we use insertion sorting

Insertion sorting is adaptive, which means if array is sorted the number of steps will be reduced.
Number of swapping is less compared to Bubble sort
It can be used in Hybrid sorting algorithms, where Hybrid refers to internally built sorting techniques.

Code Snippet example

static void insertioSort(int[] arr){
        for(int i = 0; i < arr.length-1; i++){
            for(int j = i+1; j < 0; j--){
                if(arr[j] < arr[j-1]){
                    int temp = arr[j];
                    arr[j] = arr[j-1];
                    arr[j-1] = temp;
                }else{
                    break;
                }
            }
        }
    }

Thank you for reading, Please like the article, It will encourage me to write more such articles. Do share your valuable suggestions, I appreciate your honest feedback!!

Sorting — Algorithm in Java — 1